firewalld防火墙(一)
本文共 2833 字,大约阅读时间需要 9 分钟。
实验案例:基于区域、服务、端口的访问控制
实验环境 某公司的Web服务器、网关服务器均采用Linux CentOS 7.3操作系统,如图所示。为了加强网络访问的安全性,要求管理员熟悉firewall防火墙规则的编写,以制定有效、可行的主机防护策略。 实验拓扑: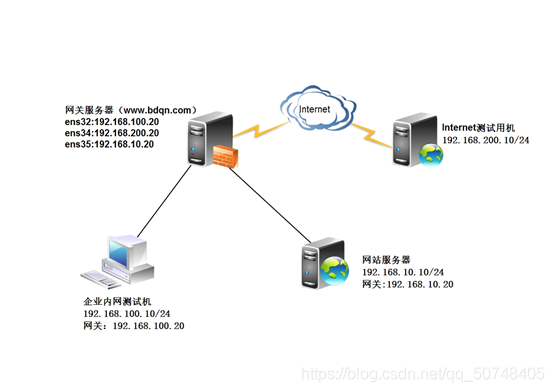
需求描述:
网关服务器ens33网卡分配到trusted(信任)区域,ens34网卡分配到external(外部)区域,ens35网卡分配到dmz(非军事)区域。 网站服务器和网关服务器将ssh默认端口都改为12345 网站服务器开启https,过滤未加密的http流量,且拒绝ping。 实验步骤: Step①基本环境配置 (1)为网关服务器与网站服务器配置主机名及网卡地址 网关服务器: [root@Centos ~]# hostnamectl set-hostname trusted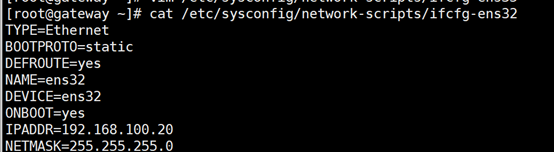
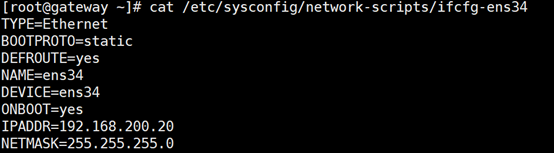
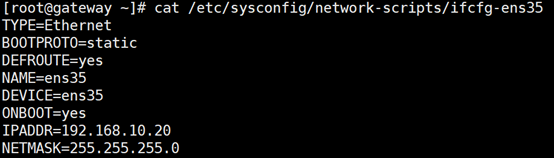
企业内网测试机:
[root@trusted ~]# hostnamectl set-hostname trusted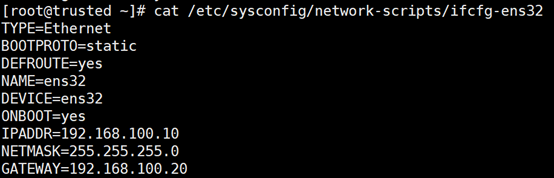
Internet测试用机
[root@externsl ~]# hostnamectl set-hostname externsl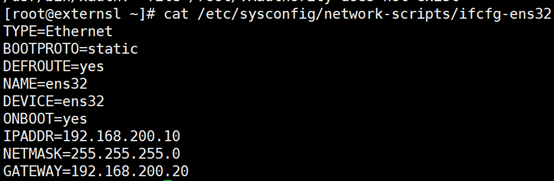
网站服务器:
[root@dmz ~]# hostnamectl set-hostname dmz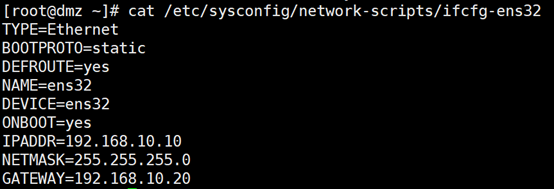
更改SSH的监听端口
网关改ssh端口 [root@gateway ~]# vim /etc/ssh/sshd_config 网站改ssh端口 [root@dmz ~]# vim /etc/ssh/sshd_config
[root@gateway ~]# systemctl restart sshd //重新启动服务
(2)开启网关服务器的路由转发功能 [root@gateway ~]# vim /etc/sysctl.conf
Step②在网站服务上部署web站点
(1) 安装httpd和mod_ssl软件包 [root@dmz ~]# yum -y install httpd mod_ssl (2) 启用并启动httpd服务 [root@dmz ~]# systemctl start httpd [root@dmz ~]# systemctl enable httpd (3) 创建网站测试页 [root@dmz ~]# echo “this is a test web” >> /var/www/html/index.html Step③为网站服务和网关服务编写firewalld规则 (1) 网站服务规则 1) 开启并启动firewall [root@dmz ~]# systemctl start firewalld [root@dmz ~]# systemctl enable firewalld 2) 将默认区域改为dmz [root@dmz ~]# firewall-cmd --set-default-zone=dmz 查看默认区域 [root@dmz ~]# firewall-cmd --get-default-zone Dmz 3) 为dmz区域打开https服务及添加TCP的12345端口 [root@dmz ~]# firewall-cmd --zone=dmz --add-service=https --permanent [root@dmz ~]# firewall-cmd --zone=dmz --add-port=12345/tcp --permanent (–permanent为设置永久性规则) 4)禁止ping [root@dmz ~]# firewall-cmd --add-icmp-block=echo-request --zone=dmz –permanent 5) 因为预定义的ssh更改了默认端口,所以将预定义ssh服务移除 [root@dmz ~]# firewall-cmd --zone=dmz --remove-service=ssh –permanent 6) 重新加载firewalld激活配置,并查看 [root@dmz ~]# firewall-cmd –reload [root@dmz ~]# firewall-cmd --list-all --zone=dmz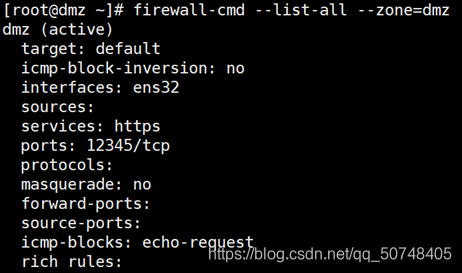
(2)在网关服务器上配置firewalld防火墙
1)启动并启用防火墙 [root@gateway ~]# systemctl start firewalld [root@gateway ~]# systemctl enable firewalld 查看防火墙状态 [root@gateway ~]# firewall-cmd --state running 2)设置默认区域为external区域,并查看配置结果 [root@gateway ~]# firewall-cmd --set-default-zone=external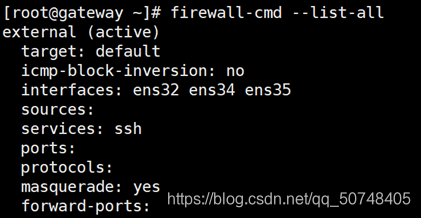
4) 将ens32网卡配置到trusted区域,将ens35配置到dmz区域
[root@gateway ~]# firewall-cmd --change-interface=ens32 --zone=trusted [root@gateway ~]# firewall-cmd --change-interface=ens35 --zone=dmz 查看配置 [root@gateway ~]# firewall-cmd --get-active-zones
5) 配置external区域添加TCP的12345端口
[root@gateway ~]# firewall-cmd --zone=external --add-port=12345/tcp –permanent 6) 配置external区域移除SSH服务 [root@gateway ~]# firewall-cmd --zone=external --remove-service=ssh --permanent 7)配置external区域禁止ping [root@gateway ~]# firewall-cmd --zone=external --add-icmp-block=echo-request –permanent 8) 重新加载防火墙激活配置 [root@gateway ~]# firewall-cmd –reload验证;
- 在互联网测试计算机上通过SSH登录网关外部接口12345端口 [root@externsl ~]# ssh -p 12345 192.168.200.20
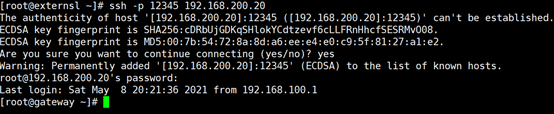
2)在企业内网测试计算机SSH登录web网站服务器的12345端口
[root@trusted ~]# ssh -p 12345 192.168.10.10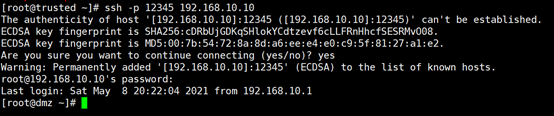
3)在企业内网测试机上访问网站服务器
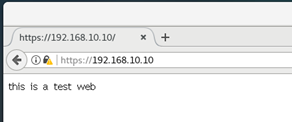
转载地址:http://wbbnz.baihongyu.com/
你可能感兴趣的文章
Navicat工具Oracle数据库复制 or 备用、恢复功能(评论都在谈论需要教)
查看>>
navicat怎么导出和导入数据表
查看>>
Navicat报错:1045-Access denied for user root@localhost(using passwordYES)
查看>>
Navicat通过存储过程批量插入mysql数据
查看>>
Navicat(数据库可视化操作软件)安装、配置、测试
查看>>
NB-IOT使用LWM2M移动onenet基础通信套件对接之APN设置
查看>>
NBear简介与使用图解
查看>>
nc命令详解
查看>>
ndk特定版本下载
查看>>
NDK编译错误expected specifier-qualifier-list before...
查看>>
Neat Stuff to Do in List Controls Using Custom Draw
查看>>
Necurs僵尸网络攻击美国金融机构 利用Trickbot银行木马窃取账户信息和欺诈
查看>>
NeHe OpenGL教程 07 纹理过滤、应用光照
查看>>
NeHe OpenGL教程 第四十四课:3D光晕
查看>>
Neighbor2Neighbor 开源项目教程
查看>>
neo4j图形数据库Java应用
查看>>
Neo4j图数据库_web页面关闭登录实现免登陆访问_常用的cypher语句_删除_查询_创建关系图谱---Neo4j图数据库工作笔记0013
查看>>
Neo4j图数据库的介绍_图数据库结构_节点_关系_属性_数据---Neo4j图数据库工作笔记0001
查看>>
Neo4j安装部署及使用
查看>>
Neo4j电影关系图Cypher
查看>>